マスターの独り言

 凍結破損のメカニズム2 (凍結破損裁判その3)

【2015/02/23(月)】

 [凍結破損関連]

<<凍結破損裁判(その2)>>　の続き

前回は水の性質と水が氷になる際に生じる体積膨張力について述べました。今回は主に水道管の強度について記述します。

※以下の文章はK技研の行った実験に対する反論として、私が記述し裁判所に提出した（はずの）書類を元にしています。今回Webに公開するにあたり、K技研の実験結果を公表しても良いのか不明であることから、その情報不足を補うため加筆訂正を行い、また言い回しやレイアウトの変更もしています。

※研究者でも無い者が記述した文章であるため、計算ミスや事実と異なる記述があるかも知れません。文責は私にありますが、もしお気づきの点がありましたら、お知らせいただければ幸いです。

凍結破損のメカニズムについて（2）

＜物質の変形・破壊＞

物質の変形には力を緩めると元に戻る弾性変形と、元に戻らない塑性変形があります。

金属やプラスチックに力を加えていくと、ある程度までは力を抜くと元に戻りますが、弾性変形域を超えて力を加えると、塑性変形を起こして元に戻らなくなるか、組織の変形量が結合力を超えてしまい延性破壊または脆性破壊を起こします。

延性破壊とは千切れるように破壊される事で、脆性破壊とは割れるように破壊される事です。一般的に金属やプラスチック（硬質）は、引っ張り方向に力を加えていくと塑性変形が起こり、延性破壊に至りますが、焼きの入った包丁のような硬質の材料や厚みのあるものでは脆性破壊を起こすことがあります。

陶器やガラス、コンクリートなどは脆性破壊を起こす代表的なものですが、通常であれば延性破壊を起こす金属やプラスチック（硬質）なども加工硬化（ひずみ硬化）により弾性が失われた場合や、低温の元では脆性破壊が起きることはよく知られています。

＜給排水配管・設備などの破損・破裂・破壊＞

水道管（以下カラン・水道メーター・フレキシブル管・銅管・接合部：エルボなどの総称として一般的に“水道管”と称します）の中で水が凍り氷の体積膨張力によって水道管に圧力がかかった際、水道管の変形量が塑性変形の限界を超えた場合は延性破壊を、低温脆性や加工硬化（金属に応力を加えると塑性変形によって硬さが増す現象）によって弾性を失っていた場合は脆性破壊を起こすと考えられます。

ここで凍結により水道管の破壊は起きずに素材の変形量が弾性変形の範囲を超え塑性変形を起こしたとします。

次に、一旦気温が上昇し氷が水になると、体積が減った分水道管内に隙間ができますが、水圧によってこの隙間は埋まります。この状態で再び凍結が起こると、応力は弱い部分に集中しやすいことから塑性変形が更に進むと考えられます。

塑性変形した部分は応力が集中しやすく、また温度の変化による素材の伸縮から繰り返し変形が起き、加工硬化から靭性（物質のねばりを表す）が低下していくことも考えられます。

これに低温による素材の靭性低下が加わり脆性破壊が起きるか、または応力の集中によって素材の変形量が塑性変形の限界を超えて延性破壊が起きるかすれば、凍結破裂となります。

上記の趣旨を簡潔に述べると、「水道管の凍結破裂は一度の凍結で起きるとは限らない」、ということになります。

＜水道管の強度＞

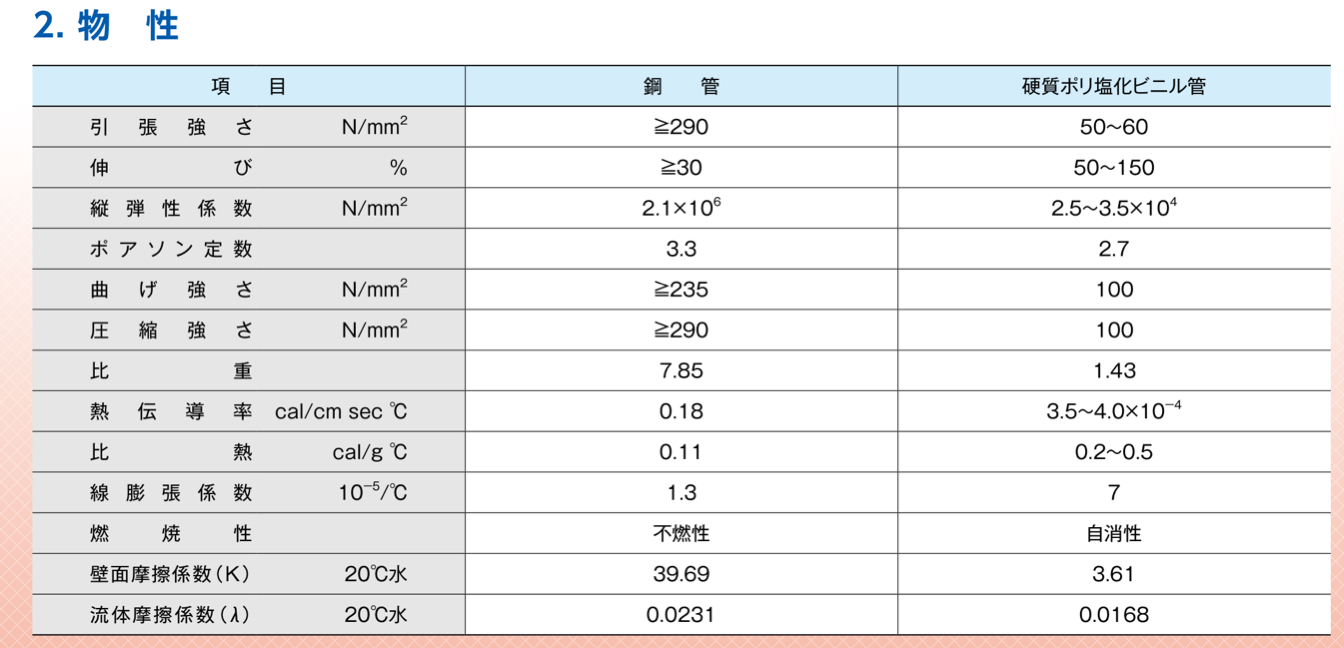
水道用硬質塩化ビニルライニング鋼管仕様書^※3の物性表よると、鋼管の引張り強さは290N/mm²(290MPa)以上、ポアソン数3.3、伸び率は30%以上となっています。

※3：http://www.nssmc.com/product/catalog_download/pdf/P018.pdf より抜粋

引張り強さとは、材料に引張り荷重を加えていった時、材料が破断に至るまでの最大応力で、材料の強度を示す最も基本的な指標となります。荷重とは外部から材料に加わる力[単位：N(ニュートン)]のことであり、これに対応して材料の内部に発生する力を応力[単位：N/mm²]と言います。

図-5：荷重の形式

http://www.nmri.go.jp/eng/khirata/design/ch02/ch02_01.html
「もの作りのための機械設計工学」より抜粋

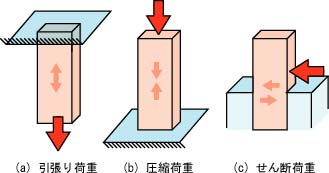
図-5の(a)(b)に示すように、力の作用面と力の作用方向とが直交するものを垂直荷重といい、作用面を引っ張る方向に作用した場合は引張り荷重、作用面を押し込むように作用した場合は圧縮荷重と呼びます。それぞれ垂直応力、引張応力、圧縮応力が対応します。また、力の作用面の法線の向きと力の作用方向が一致しない荷重をせん断荷重といい、その応力成分をせん断応力と呼びます。

図-6：材料の引張り強さのイメージ

http://www.nmri.go.jp/eng/khirata/design/ch02/ch02_01.html
「もの作りのための機械設計工学」より抜粋

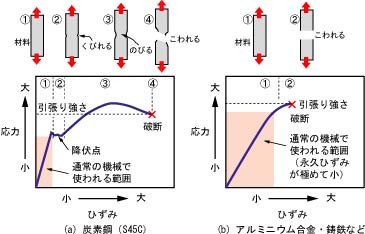
図-6は材料の引張り強さをイメージしたものです。

図-6の(a)は塑性変形を、(b)は脆性破壊を起こす材料のイメージとなります。(a)(b)どちらも(1)の範囲が弾性変形域を示します。一般に水道管に使われる鋼管は(a)の性質を持ちます。

なお、図-6(a)において、材料が破断した際の応力(4)を引張り強さとしていますが、これは間違いであり、JIS(日本工業規格)では引張り荷重(N)の最大値を原断面積(mm²)で割ったもの、つまり引張応力(N/mm²)の最大値を引張り強さと定義しています（図-7における(4)）

したがって、図-6(a)においては(3)の曲線上の最高値が引張り強さとなります。

図-7：軟鋼の引張試験結果（応力−変位線図）

http://info.shiga-irc.go.jp/public/data/130/102.pdf
「金属材料の引張試験の基礎 070612」より抜粋

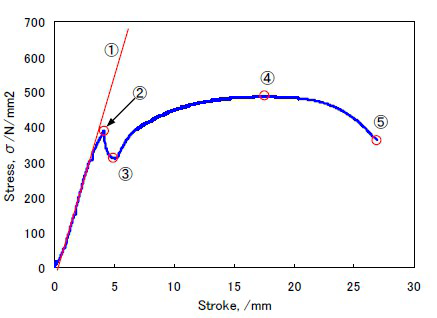
図-7は金属材料に引張荷重を加えていった際の応力-変位線図です。この図における各数字の意味は次のようになります。

(1)：弾性率

弾性変形時の応力とひずみの関係。応力に比例したひずみが生じる。

(2)：上降伏点

弾性変形から永久ひずみが蓄積される塑性変形に変わる際のもっとも高い応力値。一般に降伏圧と言えば、この上降伏点を指す。

(3)：下降伏点

上降伏点が現れた後に出てくる応力の低い状態における最低応力値。弾性変形から塑性変形に変わったあとしばらくは、低い応力で変形（ひずみ）が増す。

(4)：引張り強さ

その金属材料が持つ最大強度。下降伏点の後、応力は再び上昇し最大応力に達する。

(5)：破断点

最大応力に達した後、ひずみの増加とともに再び応力は低下し、最終的に破断する際の点。

ポアソン数とはポアソン比の逆数のことで、横ひずみと縦ひずみの比になります。

(※3の物性表において、ポアソン定数とあるのは、おそらくポアソン数の間違い)

長さL、幅Dの材料に引張り荷重を加えると、これに対応した応力(σ：シグマ)が材料内部に生じます。材料は応力に比例した断面の収縮とともに伸びが発生し、力を加える前の長さLはΔL(デルタL)だけ伸び、幅DはΔDだけ縮みます。

このとき、伸びまたは縮みの比率をひずみ(ε：イプシロン)と言います。

長さの変化を縦ひずみ(ε1)、幅の変化を横ひずみ(ε2)と言い、それぞれ次式(1)、(2)で表されます。

(1)　ε1= ΔL/L　…縦ひずみ

(2)　ε2= -ΔD/D　…横ひずみ

縦ひずみと横ひずみの比の絶対値をポアソン比(ν:ニュー)と呼び、材料によって値が異なります。また、ポアソン比の逆数をポアソン数(m)と呼びます。

ν= |ε2/ε1|　…ポアソン比

m = 1/ν　…ポアソン数

金属材料においてポアソン比が成立するのは弾性変形の範囲(図-6及び図-7の(1)であり、この間、材料の体積は増えます。ポアソン数3.3の材料に弾性変形域を超えないように引張り荷重を加えて、仮に3%伸びたとすると、体積は約1%ほど増えることになります(次式)。

ε1 = 0.03

3.3 = 0.03/ε2

ε2 ≒ 0.0091

元の体積 = L×D×D = V

L×1.03×D×0.991×D×0.991 ≒ 1.012×V

金属材料に引張り荷重を加え弾性変形を起こさせると、金属原子が作る結晶格子の並びに変化は無く、原子間距離が僅かに変わることにより変形します。引張方向では原子間距離が開き、断面の向きでは閉じるのですが、結合の制約によりその比率に差があるため、体積が増えます。

これが更に荷重を加え塑性変形域になると結晶格子は格子の欠陥である転位を生じ、スリップ、または双晶と呼ばれる現象を従って変化します。弾性変形で増えた体積は一旦元に戻り、転位の増加にしたがって体積は増えますが、その増加は僅かと考えられます。さらに荷重を加えると金属原子間の結合が一度に切れ、破断します。

注釈２：

スリップ、双晶など、金属の変形に関しての解説は複雑すぎるのと、本件に直接関与しないため割愛します。下記に参考となるものを挙げておきます。

金属の塑性変形と格子欠陥(転位)
http://ms-laboratory.jp/zai/Part2/Part2.htm

伸び率というのは、通常、引張り荷重を加えていき材料が破断した際に、力を加える前の長さと、破断した材料を繋ぎ合わせて計測した長さの比率を表します。

さて、前述に基づき、引張り荷重を加えて水道用硬質塩化ビニルライニング鋼管が破断する際の鋼管の厚みについて考察すると次のようになります。

(1)体積の変化が無いものとみなした場合、

幅(W)と厚さ(D)が同比率で減るとみなし、元の値いに対する比率をρとすると、

・伸び率 = 30%

であるから、

L×D×W = L×1.3×D×ρ×W×ρ

ρ2 = 1/1.3

ρ ≒ 0.88

(2)ポアソン比にしたがって体積が増えたと仮定した場合、

・縦ひずみε1 = 0.3
・ポアソン数 = 3.3 (ポアソン比 ≒ 0.30)

であるから、

ε1 = 0.3

3.3 = 0.3/ε2

ε2 ≒ 0.091

ρ= 1-0.091 = 0.909

以上から、この鋼管に引張り荷重を加えていった時、鋼管の厚さが元の厚さのおよそ90%未満になるとこの鋼管は破断する、と概ね考えて良いと思われます。

<<凍結破損裁判(その4)へ続く>>

最終更新日：2015/02/28(土) 08:11:13
Posted by マスター