マスターの独り言

 凍結破損のメカニズム1 (凍結破損裁判その2)

【2015/02/20(金)】

 [凍結破損関連]

<<凍結破損裁判(その1)>>　の続き

私の知人が詐欺事件の被告の一人として保険会社より訴えられた水道管の凍結破損裁判。原告側は詐欺の証拠としてK技研に依頼して行った実験結果を提出しました。

「水を満たして密封した水道用鋼管及びステンレス製フレキシブル管（以下フレキ管）を冷却したが、鋼管は-9℃、フレキ管は-14℃でも破損しなかった。故に、漏水事故が起きたとされる日時周辺の気象条件では水道管の凍結破損は起こらなかったと考えられる」

このような結論を出したこの実験は、果たして水道管の凍結破損が起こらなかった事を証明し得るのでしょうか？

前回、私はこの実験が科学的に意味を成すためには、

「水を満たして密封した水道管を冷却していけば、必ず凍結破損を起こすことが立証されていなければならない」

と、述べました。また、私が調べた限り、そのような証拠となり得るものを記述した文献は見つからなかった、とも述べました。

一方で、

「水道管に静水圧を徐々に加えていったところ、50MPaまで加えても破損しなかった。故に、この水道管は50MPaより低い水圧では破損しない」

という仮想実験を例に出し、条件付きで証拠になり得るとしました。その根拠として、

「水道管に水圧を加えていけばいずれ必ず破損することが分かっているから」

と、述べました。

この似て異なる二つの事象、どのような違いがあるのか簡単に述べると、

『静水圧による破壊実験は結果をもたらす因子が「静水圧」一つであるのに対し、管内凍結による破損の条件は温度のみでは定まらず、定量的に示すことは出来ない。』

ということになります。凍結によって水道管が破損する条件というのは単純ではないのです。

という訳で、まずは水道管が凍結により破損するメカニズムについて述べて行きたいと思います。

※以下の文章はK技研の行った実験に対する反論として、私が記述し裁判所に提出した（はずの）書類を元にしています。今回Webに公開するにあたり、K技研の実験結果を公表しても良いのか不明であることから、その情報不足を補うため加筆訂正を行い、また言い回しやレイアウトの変更もしています。

※研究者でも無い者が記述した文章であるため、計算ミスや事実と異なる記述があるかも知れません。文責は私にありますが、もしお気づきの点がありましたら、お知らせいただければ幸いです。

凍結破損のメカニズムについて (1)

＜水の性質＞

水は4℃で体積が最小（密度最大）となり、氷になると約9％程体積が増えます（線膨張で約3%※1-1）。これは水分子の間で水素と酸素が水素結合を起こし結晶化するためで、この結晶構造の隙間が多いため体積が増えます※1-2（図1）

図-1 氷の結晶構造

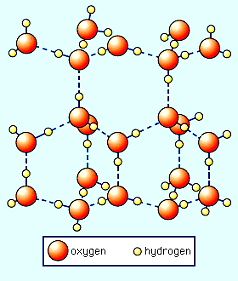
引用元：http://www.asahi-net.or.jp/~ue3t-cb/bbs/special/sience_of_hotspring/sience_of_hotspring_5-2.htm

※1-1
体積膨張率をβ(ベータ)、線膨張率をα(アルファ)とすると、「β≒3α」の関係となります。

1辺の長さがLの正立方体の体積をVとすると
        V = L3 
Lが膨張した場合の膨張率をα、この時の体積膨張率をβとすると、
        (1 + β)×V =  (1 + α)3×L3
ここでV = L3 だから
        1+β = (1+α)3
これを展開すると
        β= 3α+3α2+α3
膨張率を考えた場合、3α2+α3は十分に小さい値なので（α=0.03とすると、0.002727）
        ∴ β≒ 3α

※1-2

一つの水分子の酸素原子と別の水分子の水素原子の一つが水素結合を起こし、一つの水分子を中心に各頂点にそれぞれ水分子を一つ配した正四面体構造をとります。この水分子５個による基本構造（クラスタ）を元に結晶構造をとるのですが、繋がりの制約から六角形の隙間ができるため体積が増えます。

＜水の膨張＞

水は温度と共に体積（密度）を変化させます。
0〜33℃の間において、水の体膨張率（体積膨張率）は次の式で求められます※2

1-(0.06427×10-3)t+(8.5053×10-6)t2-(6.7900×10-8)t3

(t = ℃)

※２：出典　岩波理化学辞典

この式より0〜33℃の間における水の体膨張率と0℃に換算した体積率を表にしたのが表-1です。

表-1

温度(℃)	体膨張率	0℃体積率
0	1.0000000	1.0000000
1	0.9999442	1.0000558
2	0.9999049	1.0000951
3	0.9998819	1.0001181
4	0.9998747	1.0001254
5	0.9998828	1.0001172
6	0.9999059	1.0000941
7	0.9999436	1.0000564
8	0.9999954	1.0000046
9	1.0000610	0.9999390
10	1.0001399	0.9998601
11	1.0002318	0.9997683
12	1.0003362	0.9996639
13	1.0004527	0.9995475
14	1.0005809	0.9994194
15	1.0007205	0.9992800
16	1.0008709	0.9991298
17	1.0010318	0.9989692
18	1.0012029	0.9987986
19	1.0013836	0.9986184
20	1.0015735	0.9984290
21	1.0017723	0.9982308
22	1.0019796	0.9980243
23	1.0021950	0.9978099
24	1.0024179	0.9975879
25	1.0026481	0.9973589
26	1.0028852	0.9971231
27	1.0031286	0.9968812
28	1.0033781	0.9966333
29	1.0036331	0.9963800
30	1.0038934	0.9961217
31	1.0041584	0.9958588
32	1.0044278	0.9955917
33	1.0047012	0.9953208

この表-1において意味するところは次のようになります。

【体膨張率】
0℃で1単位（例：1000ml）の水の温度を変化させた場合の体積。

• 4℃で999.87mlとなり密度最大 
• 20℃で1001.57ml 

【0℃体積率】
0〜33℃の任意の温度における1単位（例：1000ml）の水を0℃まで冷やした時の体積。

• 4℃で1000mlの水は0℃で1000.13ml 
• 20℃で1000mlの水は0℃で998.43ml 

このように、水は温度によって体積を変えることが分かります。

＜氷の圧力＞

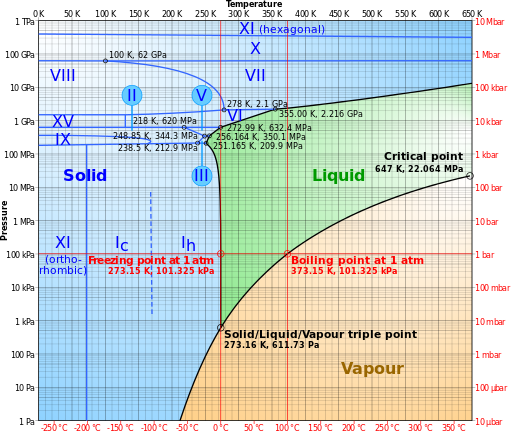
水は温度、周りの圧力により、気体、液体、固体の3つの状態を取ります。これを水の三態といいます（図-2）。

図-2：水の三態

引用元：Wikipedia

水が氷になると体積が増えます。密封容器などに水を閉じ込め温度を下げると、水が氷となり体積膨張力が生じます。

この体積膨張力と等しい圧力を水に加えると、水は完全に氷になることが出来ず、水と氷が存在する状態となります。この温度と圧力をプロットしたものが、Bridgmanの水・氷の平衡曲線とよばれるものです。

この体積膨張力は温度の低下と共に増加し、-21.985℃（251.165K）で理論上の最大値209.9MPa（約2072気圧、水深にして20,000m以上）に達します。

なお、図-2からは非常に高い圧力（2GPa以上）を加えれば、100℃以上の氷が存在する事が分かりますが、今回対象とするのはIh相の氷となります。

実際に水が氷になる際の圧力については様々な実験が行われており、理論値に近い値が記録されています。

一例としてＭ＆Ｔ総合センター情報の実験によると

-5℃で60MPa、-10℃で103MPa、-15℃で140MPa

の圧力が生じたとされています。

図-3：圧力発生の測定装置

http://www.mtc.pref.kyoto.lg.jp/ce_press/no942/researc2.htm
「凍結により発生した超高圧とその利用」より抜粋

図-4：密封容器中での水の温度と圧力の関係

---， Bridgmanの水・氷の平衡曲線
● ， 凍結昇圧法での実測値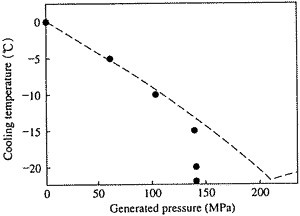　　　　

http://www.mtc.pref.kyoto.lg.jp/ce_press/no942/researc2.htm
「凍結により発生した超高圧とその利用」より抜粋

 なお、この実験において-15℃以下で圧力が頭打ちとなっていますが、これについては次のように説明されています。

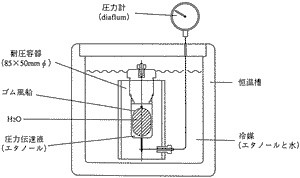
圧力がBridgmanの水・氷の平衡曲線での理論値である200MPaに到達しなかったのは水5.2に対して不凍液としてエタノール1の比率で用いたからであり、このエタノール量を減少させることにより理論値に近似してくると推定された。さらにその後（株）テラメックスに装置試作を依頼し、その協力のもと、水の状態図から得られる理論値に近い206MPa（−22℃）が得られた。なお、凍結により圧力を発生させる方法を凍結昇圧法と名付けた。

「2. 耐圧容器内での水の冷却と圧力の測定」より

 

密封容器内の水とエタノールの容積比が 5.2：1 の時に容器内の圧力は−5℃で60 MPaに、−10℃で103 MPaに、−15℃で140 MPaに達した。さらに、不凍液のエタノールの比率を減少させることにより理論値に近い、−22℃、206 MPaが得られた。

「4. まとめ」より

注釈１：

上記説明で述べられている水とエタノールの混合溶液は冷媒ではなく、圧力伝達液であることが「凍結により発生した超高圧とその利用」の「4. まとめ」を読めば分かります。圧力が頭打ちとなった原理については説明されていませんが、これは水よりエタノールの方が圧縮率が高い（同じ圧力をかけるとより小さくなる）ため、混合溶液のエタノールが縮む分、圧力が相殺されたためだと考えられます。

なお、冷媒に水は必要ないことも考えると、恐らく、図-3の冷媒と圧力伝達液の“エタノール”と“エタノールと水”の記述は逆であると思われます。

<<凍結破損裁判（その3）へ続く>>

最終更新日：2015/03/04(水) 09:08:03
Posted by マスター